[BOJ] 15686번 치킨 배달 Java 풀이

 

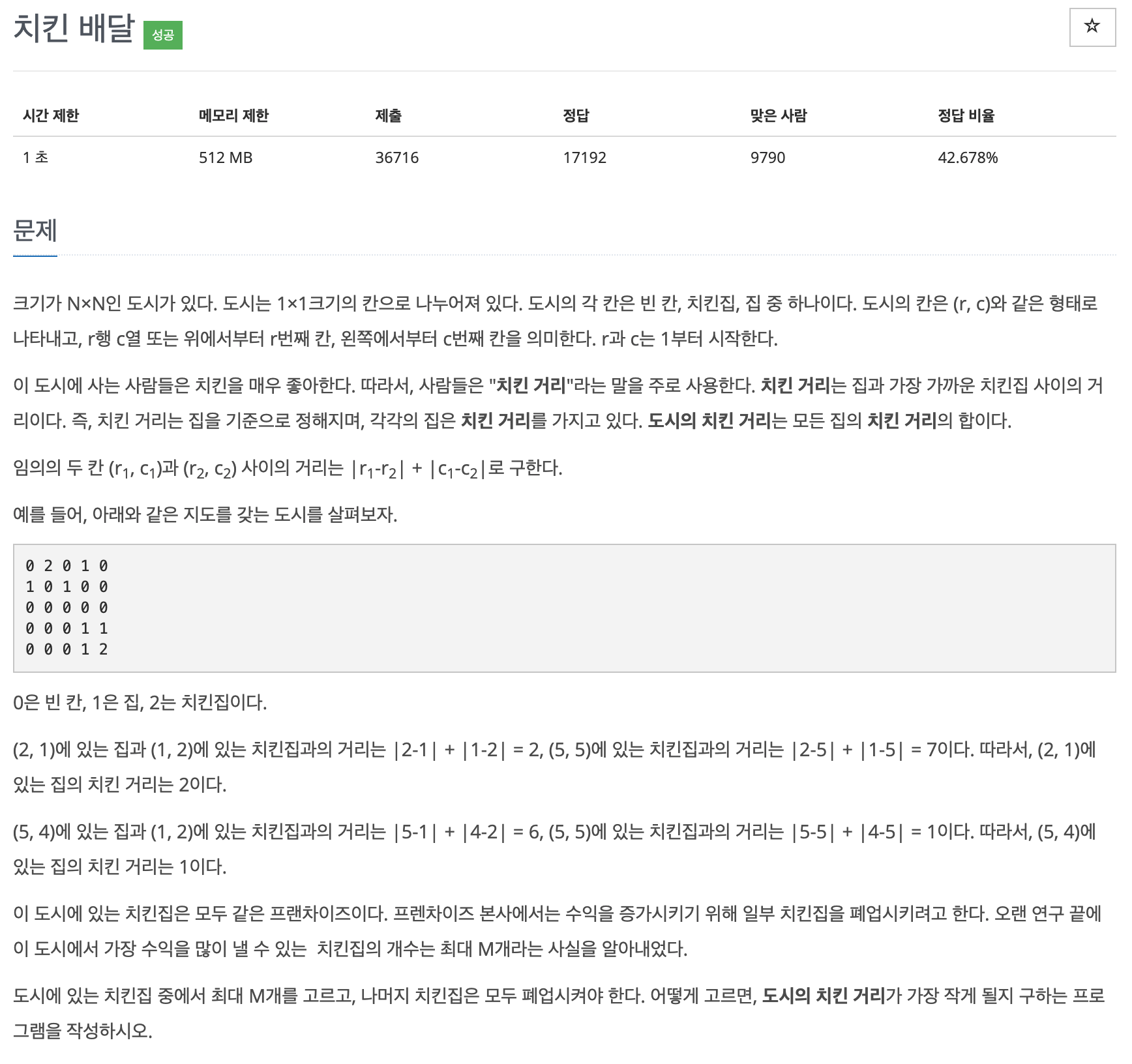
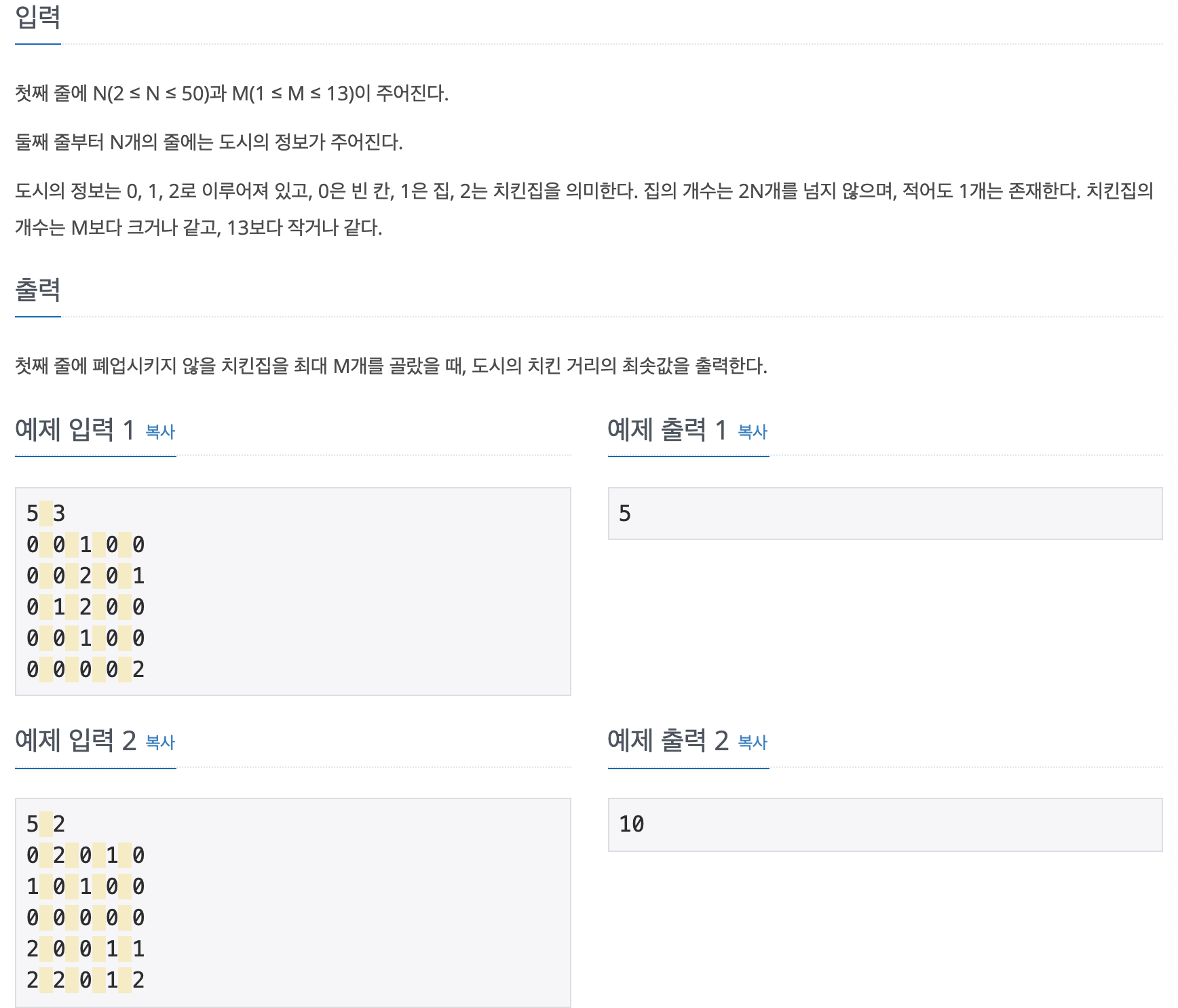
문제를 처음 풀었을 때는 시간 초과를 받고, 풀이를 약간 변형해서 통과했다. 

 

첫 번째 풀이 DFS - 시간초과

    public static void dfs(int cnt) {
		// 치킨집을 m개 오픈한 경우 도시의 치킨거리 계산
		if(cnt == m) {
			int cityDist = calculate();
			answer = Math.min(answer, cityDist);
		}
		
		// m개 미만 오픈한 경우 오픈
		for(int i = 0; i < n; i++) {
			for(int j = 0; j < n; j++) {
				if(board[i][j] == 2 && !isOpened[i][j]) {
					// 오픈해서 dfs 호출 
					isOpened[i][j] = true;
					chickens.add(new Info(i, j, 2));
					dfs(cnt + 1);
					// 호출 후 원상복구
					isOpened[i][j] = false;
					chickens.remove(chickens.size() - 1);
				}
			}
		}
	} // end of dfs

 

 

 

 

 

첫 번째 풀이에서는 전체 지도(board)의 0행 0열부터 차례대로 찾으며 열려있지 않은 치킨집을 오픈시킨다. 백트래킹 방식으로 동작하기 때문에 같은 조합의 치킨집을 오픈하더라도, 아래와 같은 케이스들이 모두 별개로 취급되어 치킨거리를 계산하게 된다.

• (1, 2), (3, 4), (4, 5)
  
  
• (1, 2), (4, 5), (3, 4)
  
  
• (4, 5), (1, 2), (3, 4)
  
  
• (3, 4), (1, 2), (4, 5)
  
  
• (4, 5), (3, 4), (1, 2)
  
  
• (3, 4), (4, 5), (1, 2)

 

만약 (1, 2), (3, 4), (4, 5) 3개의 위치에 치킨집을 오픈한다고 했을 때, 위  6가지 케이스들은 모두 같은 치킨거리를 갖게 되지만 모두 따로 계산되어 각각 치킨거리를 탐색하게 된다. 치킨집의 최대 갯수가 13개인데 위와 같이 자리를 모두 바꾼다면? 13! = 약 60억으로 시간초과가 날 수 밖에 없다.

 

이런 문제를 두 번째 문제에서 스택을 활용해 해결한다.

 

 

두 번째 풀이 DFS - 성공

    public static void dfs(int start, int cnt) {
		// 치킨집을 m개 오픈한 경우 도시의 치킨거리 계산
		if(cnt == m) {
			int cityDist = calculate();
			answer = Math.min(answer, cityDist);
		}
		
		// m개 미만 오픈한 경우 오픈
		for(int i = start; i < chickens.size(); i++) {
			Info now = chickens.get(i);
			// 오픈해서 dfs 호출
			selected.push(now);
			dfs(i + 1, cnt + 1);
			// 호출 후 원상복구
			selected.pop();
		}
	} // end of dfs

이제는 치킨집의 위치를  지도에서 꺼내지 않고, chickens라는 List에서 꺼내온다. 리스트에 미리 치킨집이 들어올 수 있는 위치들을 저장해놓고, 리스트의 인덱스를 dfs 메서드의 인자로 주고받으면서 어디부터 오픈할지를 저장해둔다. 

 

그리고, selected를 Stack으로 두면서 전체 경우의 수를 한 번씩만 탐색하도록 한다. 지도를 처음부터 선택하도록 하는 것이 아닌 인자를 하나 추가하고 다른 자료구조를 사용하는 방식으로 시간복잡도를 매우 개선할 뿐만 아니라 코드 라인 수도 줄이고 풀이도 훨씬 간결해졌다.

 

 

 

두 번째 풀이 전체 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
import java.util.StringTokenizer;

public class Main {
	static int n, m, answer;
	static int[][] board;
	static List<Info> houses = new ArrayList<>();
	static List<Info> chickens = new ArrayList<>();
	static Stack<Info> selected = new Stack<>();
	
	
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		n = Integer.parseInt(st.nextToken());
		m = Integer.parseInt(st.nextToken());
		board = new int[n][n];
		answer = Integer.MAX_VALUE;
		
		for(int i = 0; i < n; i++) {
			st = new StringTokenizer(br.readLine());
			for(int j = 0; j < n; j++) {
				board[i][j] = Integer.parseInt(st.nextToken());
				// 집이면 리스트에 추가해놓음
				if(board[i][j] == 1) {
					houses.add(new Info(i, j, 1));
				}else if(board[i][j] == 2) {
					chickens.add(new Info(i, j, 2));
				}
			}
		}
		dfs(0, 0);
		System.out.println(answer);
	}
	
	public static void dfs(int start, int cnt) {
		// 치킨집을 m개 오픈한 경우 도시의 치킨거리 계산
		if(cnt == m) {
			int cityDist = calculate();
			answer = Math.min(answer, cityDist);
		}
		
		// m개 미만 오픈한 경우 오픈
		for(int i = start; i < chickens.size(); i++) {
			Info now = chickens.get(i);
			// 오픈해서 dfs 호출
			selected.push(now);
			dfs(i + 1, cnt + 1);
			// 호출 후 원상복구
			selected.pop();
		}
	} // end of dfs
	
	public static int calculate() {
		int cityMinDist = 0;
		// 집을 하나씩 골라
		for(int i = 0; i < houses.size(); i++) {
			Info nowHouse = houses.get(i);
			int minDist = Integer.MAX_VALUE;
			// 치킨집마다 거리를 계산하고 최소 치킨거리 갱신 가능하면 갱신
			for(int j = 0; j < selected.size(); j++) {
				Info nowChicken = selected.get(j);
				// 현재 집과 치킨집 거리 계산
				int dist = Math.abs(nowHouse.row - nowChicken.row) 
						+ Math.abs(nowHouse.col - nowChicken.col);
				// 최소 치킨거리 갱신 가능하면 갱신
				minDist = Math.min(dist, minDist);
			}
			// 현재 집에서 가장 가까운 치킨거리를 도시 치킨거리에 반영
			cityMinDist += minDist;
		}
		return cityMinDist;
	}
	

}
class Info{
	int row, col;
	int type;
	public Info(int row, int col, int type) {
		this.row = row;
		this.col = col;
		this.type = type;
	}
	@Override
	public String toString() {
		return "Info [row=" + row + ", col=" + col + ", type=" + type + "]";
	}
}