[BOJ] 1753 최단경로 Java 풀이

 

 

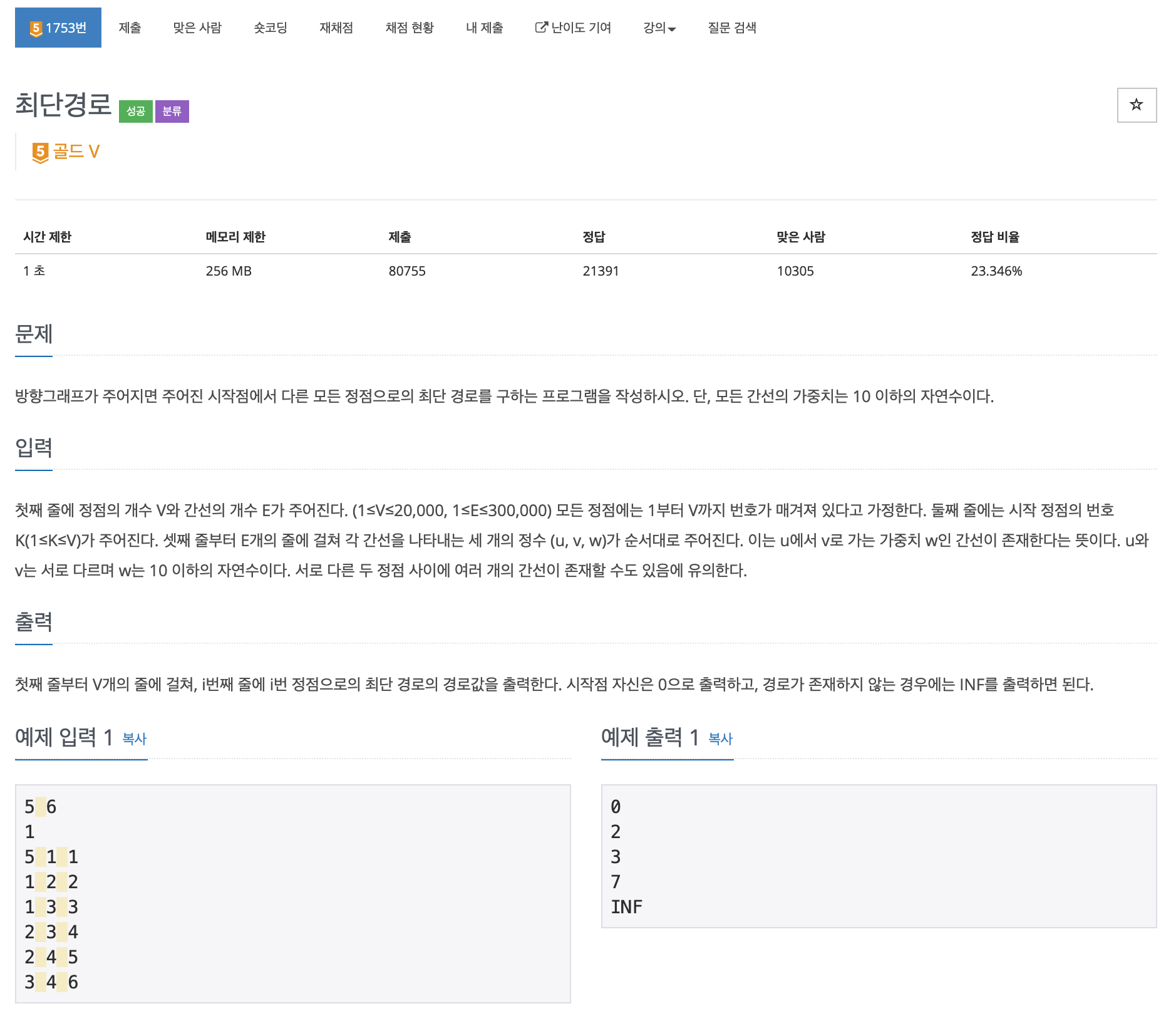
BOJ 1753 최단경로

 

제목부터 최단경로다. 최단경로와 관련된 알고리즘으로는 대표적으로 1) 다익스트라, 2) 벨만포드 , 3) 플로이드 워셜 알고리즘이 있음을 알고 각각의 특징에 대해서도 익혀두는 것이 좋다.

이 문제는 먼저 간선의 범위가 자연수이고, 시작점이 하나로 주어지므로 Dijkstra 알고리즘을 적용하는 것이 좋다. 물론 벨만포드나 플로이드 워셜 알고리즘으로도 최단 경로를 구할 수는 있겠지만 각 알고리즘의 시간복잡도를 이 문제에 적용해보면 벨만포드는 O(E log V), 플로이드 워셜 O(N^3)이므로 시간 제한에 걸리게 된다.

다익스트라 알고리즘을 적용하면 크게 어렵지 않게 풀어낼 수 있는데, 구체적인 구현 방법에 대해 잘 기억하는 것이 중요할 수 있겠다. 

(최단 경로인데 간선의 가중치가 10 이하 자연수이므로, 최악의 경 20,000개의 정점이 일렬로 늘어선 그래프여도 최단 경로는 20만 이하라서 넉넉하게 30만으로 주었다.)

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;


public class Main {
	static int V, E;
	static int start;
	static int[] dist;
	static ArrayList<Node> adj[];
	static PriorityQueue<Node> pq = new PriorityQueue<>();
	
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		StringBuilder sb = new StringBuilder();
		
		V = Integer.parseInt(st.nextToken());
		E = Integer.parseInt(st.nextToken());
		
		start = Integer.parseInt(br.readLine());
		
		// initialize
		dist = new int[V + 1];
		adj = new ArrayList[V + 1];
		
		int INF = 300000;
		
		for(int i = 1; i <= V; i++) {
			dist[i] = INF;
			adj[i] = new ArrayList<>();
		}
		
		// input processing
		for(int i = 0; i < E; i++) {
			st = new StringTokenizer(br.readLine());
			int u = Integer.parseInt(st.nextToken());
			int v = Integer.parseInt(st.nextToken());
			int w = Integer.parseInt(st.nextToken());
			
			adj[u].add(new Node(v, w));
		}
		
		// dijkstra alg
		dijkstra(start);

		
		// output processing
		for(int i = 1; i <= V; i++){
			if(dist[i] == INF) {
				sb.append("INF\n");
			}else {
				sb.append(dist[i]+"\n");
			}
		}
		System.out.println(sb.toString());
		
	}// end of main
	
	private static void dijkstra(int start_node) {
		
		dist[start_node] = 0;
		pq.add(new Node(start_node, 0));
		
		while(!pq.isEmpty()) {
			// 1. 큐에서 꺼낸다.
			Node cur = pq.poll();
			
			// 예외 처리 -> 방문한 적 있으면 건너 뜀
			if(dist[cur.node_num] < cur.node_dist) continue;
			
			// 3. 연결된 곳 순회
			for(int i = 0; i < adj[cur.node_num].size(); i++) {
				Node next = adj[cur.node_num].get(i);
				
				// 4. 갈 수 있는가(갱신할 수 있는가)
				if(cur.node_dist + next.node_dist < dist[next.node_num]) {
					// 5. 간다. + 체크아웃
					dist[next.node_num] = cur.node_dist + next.node_dist;
					pq.add(new Node(next.node_num, dist[next.node_num]));
				}
			}
			
			

		}
	}
}

class Node implements Comparable<Node>{
	int node_num, node_dist;

	public Node(int node_num, int node_dist) {
		this.node_num = node_num;
		this.node_dist = node_dist;
	}

	@Override
	public int compareTo(Node o) {
		if(this.node_dist < o.node_dist) {
			return -1;
		}else if(this.node_dist >o.node_dist){
			return 1;
		}else {
			return 0;
		}
	}
}