[BOJ] 1463 1로 만들기 Java 다시 풀기

 

BOJ 1463 1로 만들기

 

블로그에 같은 문제를 2번씩 올리는 사람이 나말고 또 있을까..?

분명 풀어서 풀이 업로드까지 해놓았는데, 거의 정확히 1년이 된 오늘 다시 푸는데 엄청 애를 먹었다.
단순한 문제 풀이가 아니라, DP를 활용함에 있어 중요한 부분인듯 싶어 고민했던 부분을 다시 기록하려 한다.

문제를 보자마자 처음 든 생각은 1이 될 때까지 입력값을 if 문으로 1번 연산(3으로 나눔) 먼저, 다음은 2번 연산(2로 나눔), 두 연산 모두 안되는 경우 3번 연산(-1)으로 처리하면서 과정을 count하면 될 거라고 생각했다.

역시 이렇게 간단할 리가 없다. 예제 입력 2처럼 10 -> 9 -> 3 -> 1 로 먼저 3번 연산을 하는 경우가 최솟값을 반환하는 경우가 있기 때문이다.

여기까지 보고 나서 바로 든 해결 방법은 '백트래킹'이다. 재귀를 통해서 모든 케이스를 전부 탐색해보고 최솟값을 return하는 것이다.
다만 이렇게 구현하면 문제는 시간복잡도인데, 혹시나 해서 확인해보니 X의 범위는 100만으로 크지 않은데, 시간 제한이 0.15초다. 백트래킹으로 3가지 연산 결과를 모두 탐색해보도록 구현하면 완전탐색(브루트포스)이기때문에 O(3^100만)으로 무조건 시간 제한이 날 것을 예상할 수 있었다.

다만 우선은 구현해놓고, 메모이제이션을 넣어놓으면 시간복잡도는 개선될 수 있기 때문에 우선은 구현해봤다.

 

완전 탐색 - 시간 제한

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class IncorrectAnswer {
	static int N;
    
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		N = Integer.parseInt(br.readLine());
		
		dp = new int[N + 1];
		
		int ans = solve(N, 0);
		
		System.out.println(ans);
	}
    
	private static int solve(int num, int cnt) {
		
		// 도착지 -> 현재까지의 count 반환 
		if(num == 1) {
			return cnt;
		}
		
		// 가장 많이 탐색해도 N을 넘어가지 않음
		int result1 = N+1;
		int result2 = N+1;
		int result3 = N+1;
		
		// 1, 2, 3번 선택한 결과의 최선 결과를 저장
		if(num % 3 == 0) {
			result1 = solve(num/3, cnt+1);
		}
		if(num % 2 == 0) {
			result2 = solve(num/2, cnt+1);
		}
		
		result3 = solve(num-1, cnt+1);
		
		
		// 각 결과값을 비교해 그 중에서의 최솟값 선택하고 저장
		int min = Math.min(result1, Math.min(result2, result3));
		
		//	현재 위치에서의 최솟값을 반환
		return min;
	}
}

 

예제 입력에 대한 출력은 정확하게 반환하지만 제출해보니 역시 시간 초과 결과를 받았다. solve 함수가 1번 연산, 2번 연산, 3번 연산을 수행하는 각각의 경우(result1, result2, result3)에 대해 재귀적으로 탐색하고, 최소 결과를 return 하는 구조로 작성했다. 

여기에서 dp를 도입했는데, 이 과정에서부터 고생 시작이었다.

처음엔 매우 간단할 줄 알았다. dp배열로 각 위치에서 최솟값을 저장해놓고 다시 그 위치를 방문하는 경우엔 더 연산을 하지 않고 저장한 값을 꺼내도록 하면 되기 때문이다.

 

DP 적용 - 예제 2 실패

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class IncorrectAnswer {
	static int N;
	static int dp[];
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		N = Integer.parseInt(br.readLine());
		
		dp = new int[N + 1];
		
		int ans = solve(N, 0);
		
		System.out.println(ans);
	}
	private static int solve(int num, int cnt) {
		
		// 도착지 -> 현재까지의 count 반환 
		if(num == 1) {
			return cnt;
		}
		
		// 현재 위치를 방문한 적이 있다면 최선의 값이 저장되어 있으므로 더 탐색하지 않음
		if(dp[num] != 0) {
			return dp[num];
		}
		
		// 가장 많이 탐색해도 N을 넘어가지 않음
		int result1 = N+1;
		int result2 = N+1;
		int result3 = N+1;
		
		// 1, 2, 3번 선택한 결과의 최선 결과를 저장
		if(num % 3 == 0) {
			result1 = solve(num/3, cnt+1);
		}
		if(num % 2 == 0) {
			result2 = solve(num/2, cnt+1);
		}
		
		result3 = solve(num-1, cnt+1);
		
		
		// 각 결과값을 비교해 그 중에서의 최솟값 선택하고 저장
		int min = Math.min(result1, Math.min(result2, result3));
		dp[num] = min;
		
		//	현재 위치에서의 최솟값을 반환
		return min;
	}
}

작성은 쉽게 했는데, 어찌된 영문인지 예제 입력2를 통과하지 못하고 4라는 출력을 보게 됐다. 그래서 solve문 내에 아래와 같은 테스트용 출력 코드를 추가해서 돌려봤다.

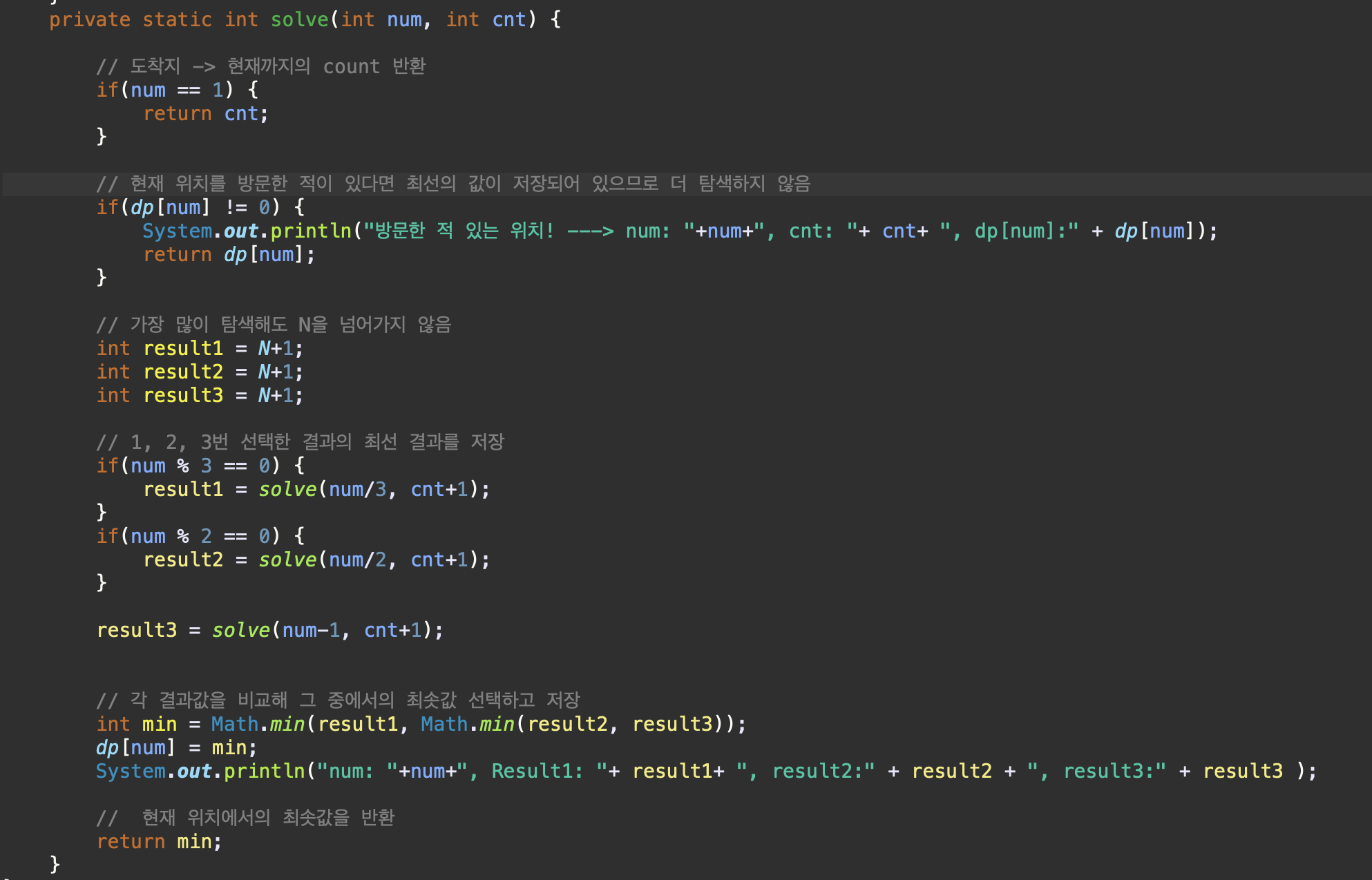
입력 10에 대한 테스트 결과

이건 뭐지...? dp[2] = 4, dp[3] = 4 ... 로 알 수 없는 결과 값이 나오고 있었다. 테스트 출력만 보고서는 상황이 잘 이해되지 않아 직접 상황을  노트에 그려봤다. 

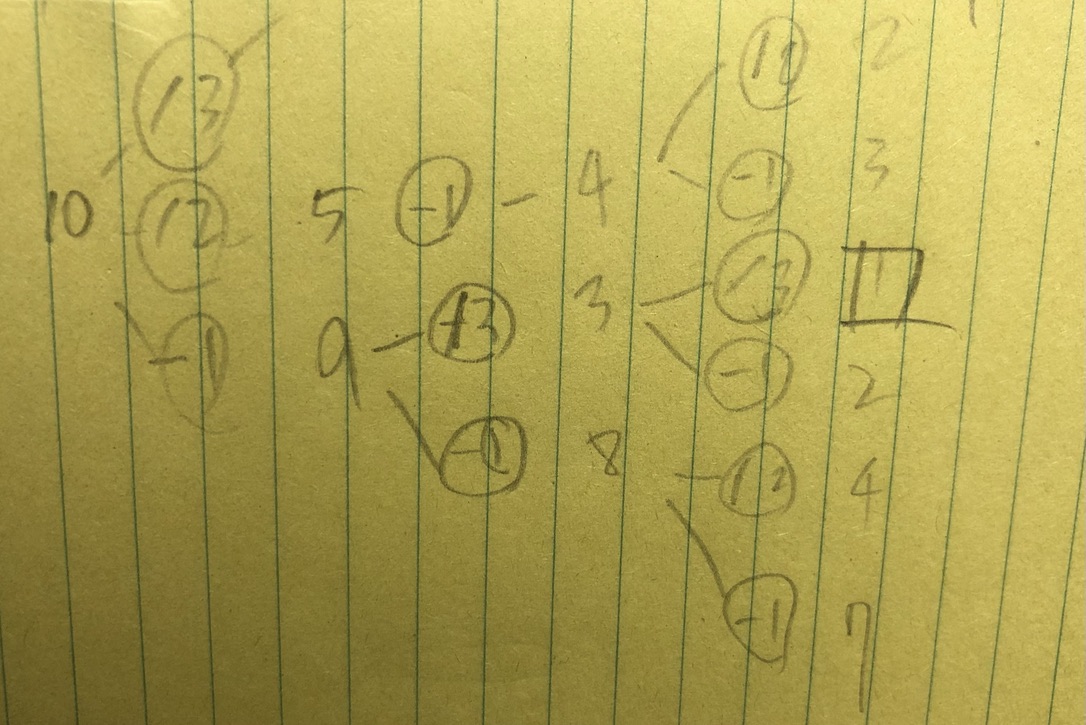
글씨가...

10에서 출발할 때 가능한 연산이 3개 중 2개 있고 5와 9가 그 결과로서 다음 턴을 시작한다. 쭉 찾아가서 1을 찾게되면 찾아온 거리를 가지고 return하면 된다.

나는 10에서 내려갈 때마다 카운트를 세고 그 위치에서의 최솟값을 dp배열에 저장하도록 만들었는데, 문제는 그 최솟값이 내가 내려온 경로를 토대로 생성된다는 점이었다. 즉 예를 들면 그림에서 10 -> 5 -> 4라는 위치에 있다면 dp[4]는 2번 연산이나 3번 연산의 결과 값중 최소결과로 저장되는데, 그 값이 10 -> 5 -> 4로 오는 경로에 영향을 받는 구조인 것이다. 

여기까지 오고 나니, Top-down방식으로는 해결할 수 없는 문제인듯 했다. count를 내려오면서 세는 것이 아니라 아래서부터 dp를 차례로 저장하면서 올라오도록 만들어야만 해결할 수 있을 것 같았다. 

다만, Bottom-up으로 문제를 구성하면 1부터 N까지 반복문을 돌려야하기에 시간 복잡도가 걱정되었는데, O(N)이라 0.01초로 무리 없이 통과할 수 있겠다는 생각이 들었고 실제로 구현도 더 간단하게 코드를 작성해 통과할 수 있었다.

 

Bottom up - 통과

public class Main {
	static int N;
	static int dp[];
	
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		N = Integer.parseInt(br.readLine());
		
		dp = new int[N + 1];
		
		dp[0] = 0;
		dp[1] = 0;
		
		// bottom-up으로 각 연산 방식을 비교하면서 최솟값을 세팅
		for(int i = 2; i <= N; i++) {
			dp[i] = dp[i - 1] + 1;
			if(i % 2 == 0) dp[i] = Math.min(dp[i/2] + 1, dp[i]);
			if(i % 3 == 0) dp[i] = Math.min(dp[i/3] + 1, dp[i]);
		}
		
		System.out.println(dp[N]);
	}

}

 

 

 

 

문제는 해결했지만 다시 고민해봤다.

정말 Top down으로는 풀 수 없는 문제일까? 여기서부터 이 문제를 다시 포스팅하는 핵심적인 이유다.

그 해결법은 아래 사진으로 확인할 수 있다.

 

좌 - 오답, 우 - 정답

 

 

왼쪽은 먼저 시도했다가 해결하지 못했던 코드이고, 오른쪽은 문제를 개선해 정답 결과를 받은 코드다. 

핵심적인 차이는 dp[]에 값을 저장하는 원리다.

 

왼쪽 코드는 재귀적으로 함수를 호출하는 시점마다 카운트를 세고, 1이 되면 경로의 카운트를 기준으로 자신을 호출했던 dp값들을 저장시켰다. 그래서 처음으로 1이 되는 순간에 1을 호출했던 2, 3 등등이 그 경로가 최솟값이 아닌데도 불구하고 해당 위치에서 dp를 셋팅해버려서 최솟값을 제대로 찾지 못한 것이다.

오른쪽 코드는 아예 재귀적으로 전달하는 카운트 매개변수를 지워버렸다. 반대로 dp값의 저장을 1이 되면 0부터 자신을 부른 값들의 순서를 올라가며 저장시켰다. 이런 방식으로 값을 저장하니 dp[]가 항상 최솟값일 수밖에 없다.

 

 

PS.

문제를 처음 접한 순간부터 Top down 방식 코드를 개선하기까지 약 3시간 넘게 걸렸다. 문제의 난이도가 이렇게까지 시간을 들이기에 적합한지는 모르겠다. 다만 이 문제를 풀면서 dp 배열을 다루거나 재귀함수 활용에 대한 경험이 앞으로 dp 문제를 풀어 나가는데 큰 도움이 될 것 같아 공유하고 싶었다.

앞으로도 쉬운 길 말고, 어려운 길 골라가서 쑥쑥 성장하자!!