[BOJ] 11726 2xn타일링 Java 풀이

BOJ 11726 2xn 타일링

 

이 문제는 문제가 dp 적용 가능함을 파악한 뒤, 점화식을 찾아내는 것이 중요하다.

N의 크기가 증가할수록 오른쪽으로 전체 직사각형이 길어지고, 이전 크기(N-1, N-2)와의 연관성을 지니고 있다.

이 때문에, 특정 2xN 크기의 타일링 방법의 수를 구할 때 재귀적으로 이전 크기의 값들을 통해 구할 수 있으며(Divide & Conquer), 한 번 계산한 값들을 저장해놓고 재사용해 연산의 숫자를 줄여줄 수 있다(Memoization).

여기까지 알아도, 구체적으로 어떤 연관성, 규칙을 가지고 있는지를 파악해야 문제를 풀 수 있다.

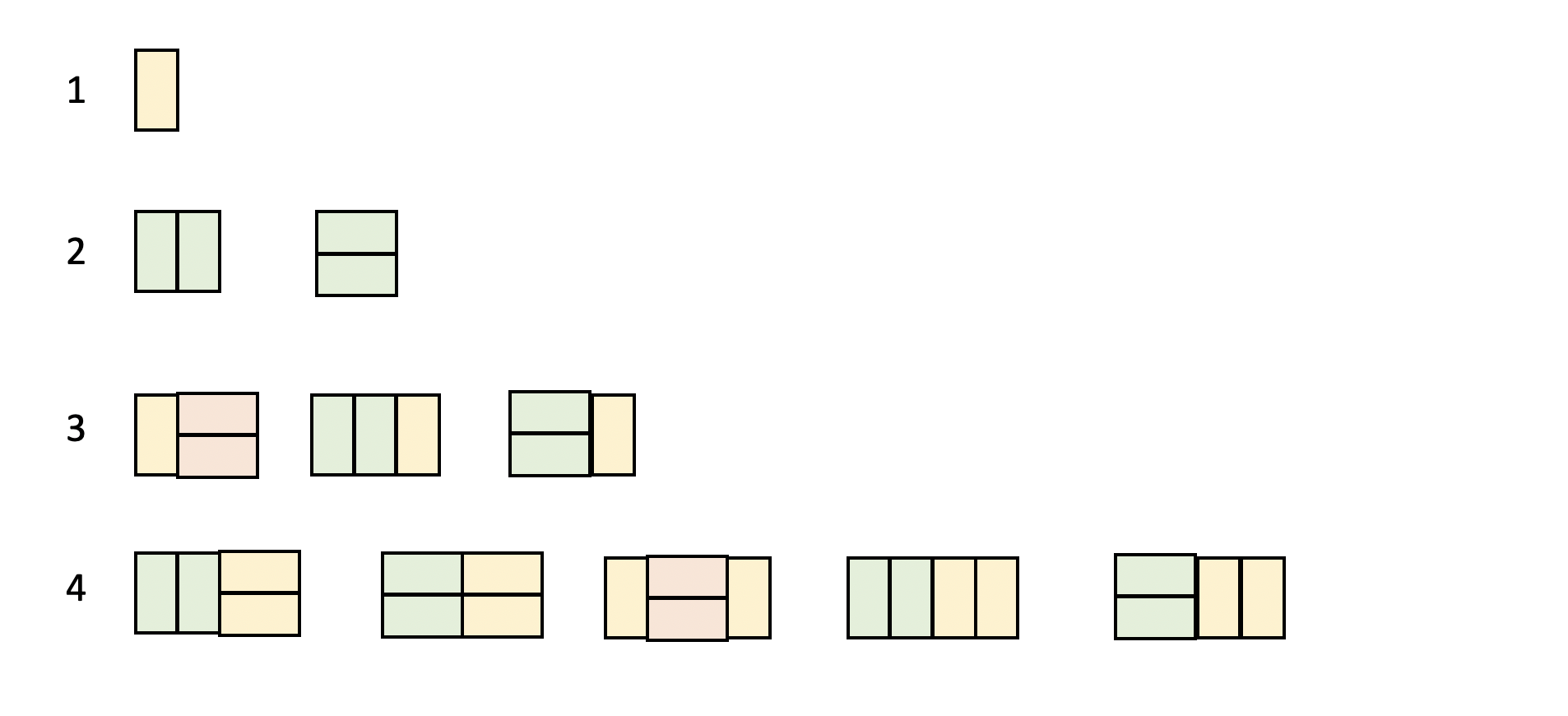
각 N의 크기별로 경우의 수를 나열했다.

N일 때의 경우의 수는 아래 두 가지 유형의 경우의 수들의 합으로 구해진다.

1. N-1일 때 경우의 수에서 오른쪽에 2 X 1 크기 타일을 붙여주는 방법으로 조건을 만족시킬 수 있다.

2. N-2일 때 경우의 수에서 오른쪽에 1 X 2 크기 타일을 2개 쌓은 형태로 붙여주는 방법으로 조건을 만족시킬 수 있다.
(2 X 1 크기 타일을 붙여주는 경우는 N-1경우에서 처리해주고, 1 X 2 크기 타일은 반드시 2개가 붙어서 추가되어야 하기 때문.)

결국 점화식은 피보나치 수열과 같은 D[N] = D[N-1] + D[N-2] 이다.

 

점화식을 알고 있다면 Bottom-up 방식이나 Top-Down 방식으로 문제를 쉽게 구현할 수 있다.

다만, 이 문제에서 배울만한 한 가지가 더 있다. '경우의 수를 10,007로 나눈 나머지를 출력하라.' 문장이다.

 

일반적으로 수가 지수 크기로 늘어나는 경우 쉽게 값이 너무 커져 숫자 표기 범위를 넘어가므로, 소수인 10007을 나눈 나머지 값을 이용하는 경우가 있다고 한다. 이 문제의 경우에서도, 값을 전부 구한 이후에 출력문에서만 %10007 연산을 해주면 오답 결과를 받는다.

이는 dp 배열을 저장하는 과정에서 이미 값이 너무 커져 가진 int 메모리에서 overflow가 일어나 값이 변형되어 저장되기 때문이다. 따라서, 유사한 문장이 문제에 나온다면, 값을 저장하는 순간부터 해당 연산을 넣어주는 것이 좋겠다.

 

 

Top Down

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class TopDown {
	// Top Down
	static int N;
	static int dp[];
	
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		N = Integer.parseInt(br.readLine());
		
		dp = new int[N + 1];
		
		dp[0] = 1;
		dp[1] = 1;
		
		solve(N);
		
		System.out.println(dp[N]);
	}
	
	static int solve(int num) {
		// 한 번 구해놓은 답이라면 더 연산 수행하지 않고 저장된 값 사용 -> Memoization
		if(dp[num] != 0) {
			return dp[num];
		}
		
		dp[num] = solve(num - 1) + solve(num - 2);
		dp[num] %= 10007;
		
		return dp[num];
	}

}

 

 

Bottom Up

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class Main {
	// Bottom Up
	static int N;
	static int dp[];
	
	public static void main(String[] args) throws Exception{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		N = Integer.parseInt(br.readLine());
		
		dp = new int[N + 1];
		dp[0] = 1;
		dp[1] = 1;
		
		if(N >= 2) {
			for(int i = 2; i <= N; i++) {
				dp[i] = dp[i - 1] + dp[i - 2];
				dp[i] %= 10007;
			}
		}
		
		
		System.out.println(dp[N]);
	}

 

마지막으로, 문제를 풀 때